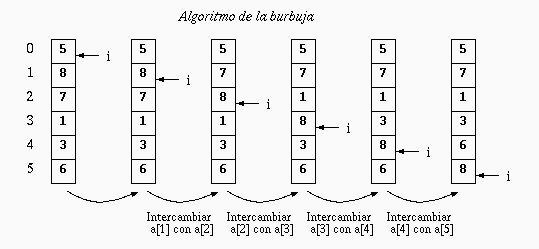
La Ordenación de burbuja (Bubble Sort en inglés)
Es un sencillo
algoritmo de ordenamiento. Funciona revisando cada elemento de la lista que va
a ser ordenada con el siguiente, intercambiándolos de posición si están en el
orden equivocado. Es necesario revisar varias veces toda la lista hasta que no
se necesiten más intercambios, lo cual significa que la lista está ordenada.
El primer procedimiento del método de la burbuja es:
Generar un ciclo que inicie desde uno hasta el número de
elementos del arreglo.
Generar un segundo ciclo dentro del anterior que inicie
desde cero hasta el número de elementos del arreglo menos dos.
Dentro del segundo ciclo debe existir una comparación que
determina el tipo de ordenamiento (ascendente o descendente) entre el primer
elemento (posición generado por el segundo ciclo) y el segundo elemento (el que
le sigue), si la respuesta a la
condición es verdadera se realiza un intercambio entre los dos elementos.
Para realizar el intercambio se genera un almacenamiento
temporal, el cual guarda el dato del primer elemento, el segundo elemento toma
el lugar del primero y en el lugar del segundo se coloca lo que contiene el
almacenamiento temporal.
Un segundo procedimiento del método de la burbuja es:
Generar un ciclo que inicie desde cero hasta el número de
elementos menos dos.
Generar un segundo ciclo desde el valor del ciclo anterior
mas uno hasta el número de elementos menos uno;
Dentro del segundo ciclo debe existir una comparación que
determina el tipo de ordenamiento (ascendente o descendente) entre el primer
elemento (posición generada por el primer ciclo) y el segundo elemento
(posición generada por el segundo ciclo), si la respuesta a la condición es
verdadera se realiza un intercambio entre los dos elementos.
Para realizar el intercambio se genera un almacenamiento
temporal, el cual guarda el dato del primer elemento, el segundo elemento toma
el lugar del primero y en el lugar del segundo se coloca lo que contiene el
almacenamiento temporal.
Un tercer procedimiento del método de la burbuja es el
siguiente:
Generar un ciclo que inicie desde uno hasta el número de
elementos menos uno.
Generar un segundo ciclo que inicie desde el número de
elementos menos uno y mientras que ese valor sea mayor o igual al del ciclo
anterior (con decrementos).
Dentro del segundo ciclo debe existir una comparación que
determina el tipo de ordenamiento (ascendente o descendente) entre el primer
elemento (posición generada por el segundo ciclo) y el segundo elemento
(posición generada por el segundo ciclo menos uno), si la respuesta a la
condición es verdadera se realiza un intercambio entre los dos elementos.
Para realizar el intercambio se genera un almacenamiento
temporal, el cual guarda el dato del primer elemento, el segundo elemento toma
el lugar del primero y en el lugar del segundo se coloca lo que contiene el
almacenamiento temporal
Ordenamiento Shell
El método se denomina Shell en honor de su inventor Donald
Shell. Su implementación original, requiere O(n2) comparaciones e intercambios
en el peor caso. . Aunque es fácil desarrollar un sentido intuitivo de cómo
funciona este algoritmo, es muy difícil analizar su tiempo de ejecución.
El algoritmo Shell sort mejora el ordenamiento por inserción
comparando elementos separados por un espacio de varias posiciones. Esto
permite que un elemento haga "pasos más grandes" hacia su posición
esperada. Los pasos múltiples sobre los datos se hacen con tamaños de espacio
cada vez más pequeños. El último paso del Shell sort es un simple ordenamiento
por inserción, pero para entonces, ya está garantizado que los datos del vector
están casi ordenados.
El procedimiento para
aplicar el algoritmo de shellsort es el siguiente:
Generar un ciclo que se encargue de controlar el tamaño que
deben tener los incrementos.
Este ciclo debe iniciar con la división del tamaño del
arreglo entre dos.
Mientras que el incremento sea mayor a cero debe continuar.
Y el cambio de incremento se elige de entre dos opciones: un
uno o la división del incremento anterior entre dos.
Un segundo ciclo dentro del anterior, controla el número de
comparaciones que se deben hacer según el tamaño del incremento.
El control de este ciclo debe iniciar con el incremento
generado anteriormente.
Mientras el control del ciclo sea menor que el tamaño del
arreglo.
El control debe cambiar de uno en uno.
Un tercer ciclo dentro del segundo controla en que momento
se detienen las comparaciones o se hacen los posibles intercambios entre los
elementos.
El control de este ciclo debe iniciar con el valor del ciclo
anterior.
Mientras que el control sea mayor o igual al incremento del
primer ciclo y el elemento del arreglo de la posición del control de este ciclo
menos el incremento, sea mayor que el elemento del arreglo de la posición
control de este ciclo, realice los intercambios entre estas posiciones.
Y el control se decremente con el valor del incremento.
Ordenamiento por
inserción
Es una manera muy natural de ordenar para un ser humano, y
puede usarse fácilmente para ordenar un mazo de cartas numeradas en forma
arbitraria. Requiere O(n²) operaciones para ordenar una lista de n elementos.
Inicialmente se tiene un solo elemento, que obviamente es un
conjunto ordenado. Después, cuando hay k elementos ordenados de menor a mayor,
se toma el elemento k+1 y se compara con todos los elementos ya ordenados,
deteniéndose cuando se encuentra un elemento menor (todos los elementos mayores
han sido desplazados una posición a la derecha) o cuando ya no se encuentran
elementos (todos los elementos fueron desplazados y este es el más pequeño). En
este punto se inserta el elemento k+1 debiendo desplazarse los demás elementos.

Ordenamiento por selección
Es un algoritmo de ordenamiento que requiere
O(n²) operaciones
para ordenar una lista de n elementos.
Su funcionamiento es el siguiente:
Buscar el mínimo elemento de la lista
Intercambiarlo con el primero
Buscar el mínimo en el resto de la lista
Intercambiarlo con el segundo
Y en general:
Buscar el mínimo elemento entre una posición i y el final de
la lista
Intercambiar el mínimo con el elemento de la posición i
De esta manera se puede escribir el siguiente pseudocódigo
para ordenar una lista de n elementos indexados desde el 1